Использование алгоритмов похожести строк в ABAP c БД HANA (AMDP) и Oracle (ADBC)
Иногда возникает необходимость сделать поиск не по точному соответствию строки, а по ее приближенному значению. Примерами могут служить ситуации удвоенной буквы «н» или необходимости поиска буквы «о» вместо введенной буквы «а». Такой поиск помогает при «огрехах» нормализации (например, когда среди кириллических символов могут встречаться латинские и наоборот). Такой поиск имеет названия «нечеткий поиск», поиск с учетом опечаток, Fuzzy Search; в своей практике я называю такой поиск «поиск с вычислением похожести», или «похожий/приближенный поиск», «поиск по похожести».
Введение
Иногда возникает необходимость сделать поиск не по точному соответствию строки, а по ее приближенному значению. Примерами могут служить ситуации удвоенной буквы «н» или необходимости поиска буквы «о» вместо введенной буквы «а». Такой поиск помогает при «огрехах» нормализации (например, когда среди кириллических символов могут встречаться латинские и наоборот). Такой поиск имеет названия «нечеткий поиск», поиск с учетом опечаток, Fuzzy Search; в своей практике я называю такой поиск «поиск с вычислением похожести», или «похожий/приближенный поиск», «поиск по похожести».
В статье будут показаны возможности использования средств ABAP для «текстового поиска похожести» для различных БД: HANA, Oracle(как 11 так и 12), а также пояснены алгоритмы, стоящие за этими возможностями. В статье будет показан подход для динамического определения степени похожести (CONTAINS( ) и FUZZY( )) и удельных весов столбцов (WEIGHT( )) на SQL-script в AMDP-классе. А также продемонстрировано использование нативных функций БД за счет ADBC – ABAP Database Connectivity. Однако лучше начать с показателей (как заметим в дальнейшем, не каждый показатель является метрикой(!)), чтобы понимать принцип и сложность вычислений в подобных алгоритмах.
В статье будут описаны возможности, доступные в ABAP, в том виде, в котором они применялись автором.
Показатели сопоставления строк/последовательностей
Для того, чтобы иметь возможность сравнивать строки «на различия», нам необходимо иметь метрики/показатели для сравнения строк. Имеется несколько подходов к измерению расстояния между последовательностями символов. Рассмотрение множества подходов выходит за рамки настоящей статьи; детально поясним лишь два из них: Расстояние Левенштейна и похожесть по Jaro-Winkler, так как именно эти два подхода реализованы в ABAP, HANA и Oracle. Остальные алгоритмы, если и реализованы, то в виде доп.разработок. Отмечу, что коннотация термина «метрика» подразумевает не просто характеризующее число, а выполнения определенных наборов требований, среди которых «неравенство треугольника». «Расстояние по Левенштейну» является метрикой; а похожесть по Жаро-Винклеру – нет.
Это минимальное количество односимвольных операций (вставки, удаления, замена), которое необходимо для превращения одного слова в другое. Другие названия этого подхода: дистанция редактирования, edit distance, Levenstein distance. Чем больше расстояние Левенштейна, тем больше строки друг от друга отличаются.
Формула для расчета выглядит так:


 Таблица 1 Пояснение к формуле расчета расстояние Левенштейна
Таблица 1 Пояснение к формуле расчета расстояние Левенштейна
|
SrcStr |
Исходная строка, длиной n |
|
TrgSrc |
Целевая строка, длиной m |
|
i, j |
i – индекс (порядковый номер) элемента строки SrcStr; 0 <= i <= n |
|
cost |
= 0, если SrcStr[i] = SrcStr[j] = 1, если SrcStr[i] <> SrcStr[j] |
|
LevensteinDistance(i,j) |
Соответствует минимуму из:
|
|
LevensteinDistance(n,m) |
Итоговое расстояние Левенштейна между строками SrcStr и TrgStr |
Подробнее можно почитать здесь, а также можно почитать в ABAP-help, так как эта функция (distance) реализована в том числе в ABAP.
Рассмотрим пример, чтобы лучше понять сам подход.
Слова «стул» и «столб». Чтобы превратить слово «стул» в слово «столб» нужно букву у заменить на букву о, и добавить букву б. Количество операций = 2 (1 замена буквы + 1 добавление буквы), значит дистанция редактирования = 2. Это очевидный пример; теперь давайте прогоним этот же пример, но по формуле выше.
Шаг1. Определение длины строк.
Первым шагом является определения длины строк. В нашем случае SrcStr = ‘стул’, в TrgStr = ‘столб’; n = 5, m = 4.
Если бы n равно 0, то расстояние было бы = m. (то есть отработали бы равенства (1), (2), (3)).
В нашем случае длины не нулевые, поэтому переходим ко 2ому шагу.
Шаг2. Построение матрицы для посимвольного анализа с начальным заполнением.
Для понимания пошагового анализа построим таблицу (матрицу).
В таблице количество столбцов будет равно количеству символов в строке-источнике (SrcStr), то есть = 4, j будет изменяться от 1 до 4; а количество строк будет равно количеству символов в целевой строке (TrgStr), то есть 5, i будет изменяться от 1 до 5.
Таблица 2 Начальное матричное представление для сравнения строк
|
с |
т |
у |
л |
||
|
0 |
1 |
2 |
3 |
4 |
|
|
с |
1 |
||||
|
т |
2 |
||||
|
о |
3 |
||||
|
л |
4 |
||||
|
б |
5 |
Шаг3. Заполнение матрицы для i = 1.
Поясним поэлементно, как будет заполняться матрица для i = 1, и j от 1 до 5
Таблица 3 Пояснение к заполнению матрицы сравнения строк для строки 1
|
Элемент исходной строки (индексируется через i) |
Элемент целевой строки (индексируется через j) |
Комментарий к расчету |
Значение ячейки |
|
SrcStr(1) = `с` |
TrgStr(1) = `с` |
Так как элементы равны между собой, то cost = 0, а это значит, что значение будет равно минимальному из предыдущих соседних ячеек (по вертикали, по горизонтали и диагонально). А именно: LevensteinDistance(1,0)=1 LevensteinDistance(0,0)=0 Значит значение будет = 0. |
0 |
|
SrcStr(1) = `с` |
TrgStr(2) = `т` |
Элементы между собой не равны => cost = 1 Минимальное значение выбираем из следующих: LevensteinDistance(0,2) + 1 = 3; LevensteinDistance(1,1) (получено на итерации выше) + 1 = 1; Значит значение будет = 1. |
1 |
|
SrcStr(1) = `с` |
TrgStr(3) = `у` |
Элементы между собой не равны => cost = 1 Минимальное значение выбираем из следующих: LevensteinDistance(0,3) + 1 = 4; LevensteinDistance(1,2) + 1 = 2; Значит значение будет = 2. |
2 |
|
SrcStr(1) = `с` |
TrgStr(4) = `л` |
Элементы между собой не равны => cost = 1 Минимальное значение выбираем из следующих: LevensteinDistance(0,4) + 1 = 5; LevensteinDistance(1,3) + 1 = 3; Значит значение будет = 3. |
3 |
Внесем значения в таблицу, отметив их цветом
Таблица 4 Матрица сравнения строк с заполненной строкой 1
|
с |
т |
у |
л |
||
|
0 |
1 |
2 |
3 |
4 |
|
|
с |
1 |
0 |
1 |
2 |
3 |
|
т |
2 |
||||
|
о |
3 |
||||
|
л |
4 |
||||
|
б |
5 |
Шаг4. Заполнение матрицы для i = 2.
Подробно расписывать уже не будем, так как принцип такой же, как и в Шаге3, но отметим цветом новые значения
Таблица 5 Матрица сравнения строк с заполненными строками 1 и 2
|
с |
т |
у |
л |
||
|
0 |
1 |
2 |
3 |
4 |
|
|
с |
1 |
0 |
1 |
2 |
3 |
|
т |
2 |
1 |
0 |
1 |
2 |
|
о |
3 |
||||
|
л |
4 |
||||
|
б |
5 |
После шага (i+2, в нашем случае = 7), таблица будет выглядеть так
Таблица 6 Матрица сравнения строк с заполненными строками и итоговым результатом
|
с |
т |
у |
л |
||
|
0 |
1 |
2 |
3 |
4 |
|
|
с |
1 |
0 |
1 |
2 |
3 |
|
т |
2 |
1 |
0 |
1 |
2 |
|
о |
3 |
2 |
1 |
1 |
2 |
|
л |
4 |
3 |
2 |
2 |
1 |
|
б |
5 |
4 |
3 |
3 |
2 |
Именно элемент с параметрами i = 5, j = 4 (то есть, самый последний элемент) и будет означать количество операций, необходимое для превращения одного слова в другое. В приведенном случае, это расстояние составляет 2.
Однако стоит обратить внимание, что количество операций хоть и показывает различие между двумя словами, но еще не характеризует степень похожести двух слов. Например, для слов «столб» и «стул», расстояние Левенштейна будет равно 2; также для слов «гречка» и «печка» расстояние будет равно 2. Можно ли сказать, что они одинаково похожи? Нет.
Нужно посчитать по формуле, учитывающую длину строк:
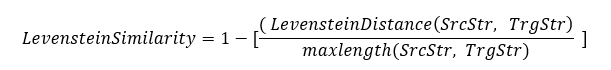

|
SrcStr |
TrgStr |
Расстояние Левенштейна |
Похожесть на основе расстояния Левенштейна |
|
стул |
столб |
2 |
1 – (2/5) = 0,6 => 60% |
|
гречка |
печка |
2 |
1 – (2/6) = 0,67 =>67% |
Таким образом, «гречка» имеет бОльшую похожесть на «печку», так как наидлиннейшее слово длиннее.
В ABAP (на уровне Application, расстояние и похожесть можно посчитать несколькими способами).
Код-Листинг 1 ABAP-Custom реализация расчета расстояния Левенштейна
|
Способ 1 (рекомендованный для понимания, но не для использования). |
|
TYPES: BEGIN OF ts_matrix_cell |
Код-Листинг 2 Реализация расчета расстояния Левенштейна через встроенную функцию ABAP
|
Способ 2 (рекомендованный для использования). |
|
METHOD abap_levenstein. |
Расстояние Левенштейна является наиболее используемым для анализа схожести строк (последовательностей). При этом применение не ограничивается сопоставлением символов естественного языка, но активно используется в биологии (например, сопоставление частей ДНК).
Происхождение метрики и алгоритма
Метрика была предложена В.И.Левенштейном в Докладе Академии наук СССР в 1965 году в статье «Двоичные кода и исправлением выпадений, вставок и замещений символов» (выдержка о введенной функции приведена на рисунке 1). Всю работу можно посмотреть, скачав по ссылке. В дальнейшем эта метрика стала синонимом термина «редакторское расстояние» (edit distance).

Рис. 1 Метрика-функция для расчета преобразования из одного слова в другое в научной работе В.И.Левенштейна 1965 (Доклад Академии наук СССР)
А вот наиболее распространенный алгоритм (рис.2) расчета был предложен в статье «The String-to-String Correction problem» Robert A.Wagner and Michael J.Fischer


Рис. 2 Алгоритм Wagner-Fischer на псевдокоде в научной статье
- Алгоритм Jaro-Winkler (Жаро-Винклера)
Имеем еще один подход для оценки сходства строк (для оценки редакционного расстояния, edit distance). Особенностью алгоритма является то, что в нем заключена поправка, чтобы учитывались совпадающие символы, не удаленные друг от друга, а также поправка, увеличивающая степень похожести за счет начального совпадения слов. Подробнее можно прочитать здесь. В компоненте S4CORE есть класс CL_RSH_MATCH_STRING, который предназначен для расчета по этому алгоритму.
Чтобы понять алгоритм, начнем с понятия «схожесть Жаро / Jaro Similarity». Этот показатель рассчитывается по формуле
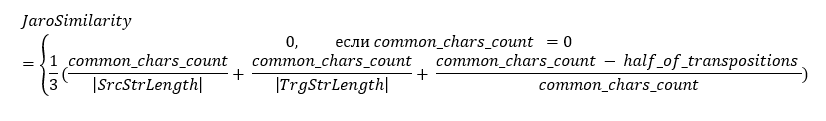
Таблица 7 Пояснение к формуле JaroSimilarity
|
Пояснения к формуле |
|
|
|SrcStrLength| |
Длина исходной строки |
|
|TrgStrLength| |
Длина целевой строки |
|
common_chars_count |
Количество совпадающих символов. Символ считается совпадающим, если они равны и находятся по номеру позиций друг от друга не далее, чем (search_range) maxSrcStrLength, TrgStrLength2-1 Обозначим этот показатель common_chars_count Здесь нужно отметить, что есть так называемая c-функция strcmp95 (написанная в том числе Винклером) (ссылка на функцию есть в настоящей статье), в которой количество совпадающих символов корректируется еще и «фонетическим совпадением» и/или ошибкой распознавания символов (например, цифра 0 и буква О) |
|
half_of_transpositions |
Половина числа всех транспозиций. Под количеством транспозиций понимается количество совпадающих символов, но у которых порядковые номера различные. |
Проведем расчет похожести Жаро для слов-имен «Алексей» и «Алексий».
Шаг1. Вычисляем длины строк и предельное отклонение порядковых номеров символов.
SrcStrLenght = 7 (для слова «Алексей»)
TrgStrLength = 7 (для слова «Алексий»)
search_range = (max(7, 7) / 2 ) - 1 = (7 / 2) – 1 = 2.
Шаг2. Вычисляем совпадающие символы.
Для наглядности сделаем таблицу и заполним ячейки по следующему способу: если символы совпадают, то в ячейку внесем 1, если нет – то 0.
|
А |
л |
е |
к |
с |
е |
й |
|
|
А |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
л |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
е |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
к |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
с |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
и |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
й |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Совпадающие элементы: (1,1), (2,2); (3,3); (4,4); (5,5); (7,7). Разница номеров у всех номеров не превышает 2, что является приемлемым для совпадения (у нас предел = 2). Получаем common_chars_count = 6.
Более того, мы рассчитали число транспозиций. Оно равно 0. Тогда half_of_transpositions = 0/2 = 0.
Шаг3. Считаем похожесть Жаро по формуле.
JaroSimilarity=13(67+ 67+ 6 -0 6)=1921=~0.905
Теперь перейдем к понятию «схожесть Жаро-Винклера». (примечание: изначально господин Жаро сделал свой подход, но господин Винклер сделал в нем улучшение для случая, когда схожесть по Jaro превышает 0.7).
WinklerSimilarity= JaroSimilarity+common_prefix_count*winkler_ratio1- JaroSimilarity
Таблица 8 Пояснение к формуле WinklerSimilarity
|
Пояснения к формуле |
|
|
JaroSimilarity |
Схожесть по Jaro, вычисленная на шаге выше (шаг3). |
|
common_prefix_count |
Количество одинаковых начальных символов в словах (например, восток и восход имеют 3 одинаковых символа вначале), но не более 4х символов |
|
winkler_ratio |
Коэффициент, равный 1/10. |
Шаг4. Вычислим одинаковый префикс для наших слов.
В нашем случае одинаковый префикс равен 4 букве «Алек» (Алексей и Алексий).
Шаг5. Рассчитаем схожесть по Жаро-Винклеру.
![]()
Шаг6 (опционально). Уточнение Винклера для длинных строк.
Этот шаг в исходной реализации Винклера имеется, однако не все библиотеки его сочли нужным реализовать. В исходной реализации данная опция включена по умолчанию, но ее можно отключить с помощью параметра на входе. В моей реализации эта опция отключена по умолчанию, и ее можно включить на входе. (переменная WinklerAdjustment_for_long_string - Корректировка для длинных строк (при выполнении определенных критериев)).


Собственно, дополнение Винклера – это поправка схожести Жаро с учетом начального совпадения строк; то есть, если строки начинаются с одинакового набора букв (но не более 4), то они считаются более похожими; если же у строк нет одинаковых начальных букв, то дополнение Винклера никак «не поднимает» схожесть строк а также уточнение для длинных строк (в случае необходимости).
Код-Листинг 3 Авторская реализация расчета похожести по Jaro-Winkler в ABAP
|
Полностью custom-способ. |
|
METHODS calc IMPORTING !iv_compare_length TYPE syindex DEFAULT 0 !iv_adjust4long TYPE abap_bool DEFAULT abap_false !iv_case_insensitive TYPE abap_bool DEFAULT abap_true !iv_phonetic_adjust TYPE abap_bool DEFAULT abap_false EXPORTING !ev_sim_jaro_winkler TYPE decfloat16 !ev_sim_jaro TYPE decfloat16 . |
|
DATA search_range TYPE syindex. DATA common_chars_count TYPE syindex. DATA half_of_transpositions TYPE syindex. DATA common_chars_incl_phonetic TYPE p LENGTH 7 DECIMALS 4. DATA common_prefix_count TYPE syindex. """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""" delete_lead_trail_spaces( ). do_upper_case( iv_case_insensitive ). cut_the_part2be_compare( iv_compare_length ). """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""" |
Если хотите прочитать статью полностью и оставить свои комментарии присоединяйтесь к sapland
ЗарегистрироватьсяУ вас уже есть учетная запись?
Войти






Обсуждения 2
2
Комментарий от
Александр Грибов
| 25 февраля 2021, 07:25
P.S. Какое-то время назад тоже пользовался нечётким поиском. Был проект по распознаванию отсканированных счетов-фактур, использовал нечёткий поиск для поиска материалов по наименованию. Cэкономили немало времени и сберегли человеческие нервы :) Наверное, тоже изложу свой наколеночный вариант в статье...
Комментарий от
Олег Башкатов
| 25 февраля 2021, 19:28
Александр Грибов 25 февраля 2021, 07:25
Олег, это не статья, но целый научный труд :) Спасибо за подробные разъяснения, за рассмотрение разных подходов, объём проделанной работы поражает. Что побудило тебя так глубоко погрузиться в вопрос?
P.S. Какое-то время назад тоже пользовался нечётким поиском. Был проект по распознаванию отсканированных счетов-фактур, использовал нечёткий поиск для поиска материалов по наименованию. Cэкономили немало времени и сберегли человеческие нервы :) Наверное, тоже изложу свой наколеночный вариант в статье...
>>>Что побудило тебя так глубоко погрузиться в вопрос?
в OData есть опция search_string и paging (top/skip) - как правило, эффективнее переложить эти задачи на БД.
>>>>Был проект по распознаванию отсканированных счетов-фактур ..... Наверное, тоже изложу свой вариант в статье...
Ждем :-) про такое молчать не стоит - нужно делиться :-)