Минимизация воздействия "сборки мусора" в среде Java на производительность системы

Рудольф Майер (Rudolf Meier)

Рудольф Майер (Rudolf Meier)

Разработчик, группа SAP по оптимизации производительности систем, управлению данными и масштабируемости, SAP AG

Рудольф Майер начал свою работу в ИТ с исследования, анализа и моделирования физических экспериментов на лабораторных ускорителях частиц по всему миру. Он вошел в группу SAP по оптимизации производительности систем, управлению данными и масштабируемости в 2004 году. В дополнение к работе над вопросами производительности ABAP, в сферу его внимания также входит производительность новых технологий пользовательских интерфейсов в мире Java. Рудольф получил степень доктора физических наук в области экспериментальной физики в Университете Карлсруэ в 1993г., и работает частным лектором в университете Тюбингена в Германии. С автором можно связаться по адресу rudolf.meier@sap.com.

Когда встает вопрос об оптимизации производительности многопользовательского приложения, приходится задуматься о самых разных аспектах программирования и оптимизации системы. Естественно в таком случае сосредоточить усилия по оптимизации на эффективных параллельных вычислениях, устраняя или снижая конкуренцию приложений. Основной момент в целевом и успешном решении подобных проблем – четкое понимание того, как приложения борются за ограниченные системные ресурсы.

В целом конкурентные условия возникают как следствие разнообразных свойств приложения или системной среды, причем каждая проблема должна решаться отдельно. Однако в приложениях Java типичной причиной таких условий является так называемая “сборка мусора” (GC). Хорошо известно, что процесс сборки мусора воздействует на производительность системы, в частности, на время отклика приложения или пользователя. Вопрос в том, насколько сильно это воздействие? Группа SAP по производительности, управлению данными и масштабируемости столкнулась с этим вопросом на ранней стадии разработки проекта, когда анализ производительности показал немасштабируемое поведение. Также наблюдалась значительная активность процесса сборки мусора. Была ли сборка мусора действительной причиной недостаточной масштабируемости? Или проблема была вызвана конкретными соревновательными условиями приложений? Какой путь следовало избрать для устранения недостатков? Все эти вопросы заставили тщательнее присмотреться к влиянию процесса сборки мусора в среде Java на производительность.

В этой статье представлены результаты нашего расследования. В ней подробно разъясняется воздействие сборки мусора на приложения, выполняемые на виртуальной машине Java (JVM), и приводится формула количественной оценки влияния сборки мусора на время отклика приложений. Этим эмпирическим правилом можно пользоваться для предсказания степени влияния сборки мусора на приложения в системе, что помогает быстро определить, вызвана ли проблема с масштабированием сборкой мусора, и, следовательно, должно ли решение сводиться к оптимизации использования памяти. Если же наблюдаемую деградацию производительности будет невозможно объяснить оценочным воздействием сборки мусора, это укажет на то, что причина заключается в чем-то еще, скорее всего – в особых конкурентных условиях, присущих приложению или системной среде.

Обратите внимание! Эта статья предназначена для разработчиков Java и системных администраторов Java. Предполагается базовый уровень знания программирования Java, среды выполнения Java и управления памятью Java.

Начнем с исследования времени отклика приложения – ключевого показателя производительности для многопользовательских приложений. Сначала кратко рассмотрим ожидаемое поведение времени отклика приложений в идеальном мире в соответствии с теорией массового обслуживания (также проведем сравнение с реальными приложениями). Затем добавим в модель процесс сборки мусора. Перед подробным рассмотрением воздействия процесса сборки мусора на выполнение приложений приведем обзор его задач и механизмов. Для количественного описания эффекта сборки мусора введем аналитические модели и моделирование по методу Монте-Карло, которые затем упростим для получения более четкого представления о воздействии процесса сборки мусора. Основной результат – эмпирическая формула для оценки влияния процесса сборки мусора на время отклика приложений. В завершение даются рекомендации по мерам, которые можно принять в случае признания процесса сборки мусора основной причиной снижения производительности в системе. Также будет уделено внимание приемам программирования с эффективным использованием памяти, которые могут применяться при разработке приложений и настройке системы.

Время отклика приложения

Время отклика приложения или пользователя – ключевой показатель производительности для многопользовательских приложений. Время отклика чувствительно к множеству параметров: от общей нагрузки на систему до соревнования приложений за доступ к базе данных. В дополнение к этим факторам на время отклика влияет общесистемная “минута тишины”, устраиваемая сборщиком мусора Java. Перед разбором эффектов сборки мусора стоит, однако, вкратце рассмотреть теоретические предположения относительно времени отклика приложений. Эти предположения проистекают из теории массового обслуживания.

Время отклика приложений и теория массового обслуживания

Теория массового обслуживания описывает поведение системы, в которой очередь заявок на обслуживание обрабатывается конечным количеством обслуживающих узлов. Теория массового обслуживания – ветвь математической теории вероятности, применимая к широкому спектру задач по организации обслуживания¹. Реальным примером системы обслуживания могут служить, например, авиапассажиры, ожидающие таможенного контроля у фиксированного числа таможенных терминалов. Теория массового обслуживания позволяет вычислить характерные количественные показатели, такие как среднее время ожидания или средняя длина очереди (в идеальных условиях).

¹ Обзор теории массового обслуживания см. в Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications (WileyInterscience, 1998). Различные материалы по теории массового обслуживания также доступны по адресу: http://www2.uwindsor.ca/~hlynka/queue.html.

В этой статье теория массового обслуживания используется для предсказания времени ожидания пользователя в многопользовательских приложениях под нагрузкой. Для получения качественной картины составляющих такого предсказания см. Рис. 1. Этот график заявок от времени иллюстрирует идеализированную нагрузку на многопользовательское приложение.

Рис. 1 Увеличение времени отклика из-за конкуренции за системные ресурсы

Для простоты в примере используется система с одним процессорным ядром. Как видно из рисунка, в системе работает определенное количество пользователей, каждому из которых соответствует временная шкала. Каждый пользователь время от времени размещает заявки на обслуживание, показанные в виде прямоугольников на временных шкалах. Если заявка немедленно начинает обрабатываться процессором и эта обработка не прерывается до ее завершения, она выполняется за время, называемое чистым временем обслуживания. Между заявками на обслуживание пользователь ожидает в течение определенного периода, называемого временем размышления пользователя. Самая нижняя из трех временных шкал пользователей показывает, что происходит в случае конкуренции двух заявок на обслуживание за внимание процессора: одна из заявок вынуждено ожидает завершения обработки другой. Это приводит к увеличению времени обслуживания.

Разумеется, среднестатистическое время отклика для всех пользователей и заявок зависит от того, насколько часто поступающие заявки пользователей совпадают по времени. Очевидно, что конфликты намного более вероятны при высокой нагрузке и большом количестве пользователей. Теперь применим теорию массового обслуживания для определения поведения среднего времени отклика при увеличении нагрузки на систему. Предполагая некоторое идеальное распределение времени между получением заявок и чистого времени обслуживания, известное как распределение Маркова², ответ находится в очереди “M/M/n” (“M” означают Марковское распределение, а “n” – количество обслуживающих узлов). Прогнозы для систем с одним и четырьмя процессорными ядрами показаны на Рис. 2 на следующей странице. Строится график относительного времени отклика (отношение среднего времени отклика к непосредственному времени обслуживания в зависимости от нагрузки на систему), а также кривые для одного процессорного ядра (пунктирная линия) и четырех ядер (сплошная линия). Очевидно, что число ядер существенным образом влияет на среднее время отклика. В то время как при 50% нагрузке время отклика пользователя в случае одного ядра удваивается, в тех же условиях на четырех-ядерной системе увеличение времени отклика составляет не более 10%. Такое поведение правдоподобно: одно из четырех ядер будет свободно с большей вероятностью, чем в случае наличия в системе единственного ядра.

² Для получения подробной информации о Марковском распределении см. Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications (WileyInterscience, 1998) и ресурсы, доступные по адресу http://www2.uwindsor.ca/~hlynka/queue.html.

Теория массового обслуживания в сравнении с реальными приложениями

Для получения прогнозов на Рис. 2 исходя из теории массового обслуживания мы рассматривали идеализированную ситуацию. В частности, нами был сделан ряд допущений относительно распределения интервалов между прибытием заявок и временем обслуживания. Итак, насколько такой модельный расчет применим к реальным условиям? Сравним его результаты с прогоном эталонного теста FI (часть набора тестов SAP³) на четырех-ядерном компьютере. На Рис. 3 показано время отклика в сравнении с прогнозом для очереди M/M/4, показанным на Рис. 2. Графики показывают, что между теорией и практикой существует чудесное сходство.

³ Подробная информация об эталонном тесте SAP FI доступна по адресу http://www.sap.com/benchmark/.

Рис. 2 Поведение времени ожидания исходя из теории массового обслуживания

Рис. 3 Время отклика, измеренное в эталонном тесте SAP FI, по сравнению с прогнозом теории массового обслуживания

Системы, которые ведут себя согласно теории массового обслуживания, обладают важным свойством с точки зрения многопользовательских приложений: масштабируемостью. Масштабируемость означает, что при добавлении пользователей в систему можно просто добавить эквивалентное количество вычислительной мощности. Более подробно о масштабируемости см. в выноске ниже.

Наоборот, прогноз теории массового обслуживания теперь можно использовать как инструмент проверки масштабируемости многопользовательских приложений. Системная нагрузка и ее относительное увеличение измеряется в терминах времени отклика и сравнивается с прогнозом.

Масштабируемость Масштабируемость приложения (или системы) в целом означает степень возможного увеличения или сокращения размеров, объемов данных или количества пользователей при сохранении способности к правильному и предсказуемому функционированию. Для реализации бизнес-требований в фактической аппаратной конфигурации приложение должно масштабироваться линейно (или лучше). Рассмотрим следующий пример линейного масштабирования: многопользовательское приложение с некоторой характеристикой времени отклика на одной системе при параллельном использовании 100 пользователями должно сохранять ту же характеристику при работе 1000 пользователей и 10-кратном увеличении ресурсов (процессора, памяти и диска).

Пример приложения Java

Рассмотрим ситуацию, которая встала перед командой по производительности, управлению данными и масштабируемости SAP на ранних этапах разработки нового многопользовательского Java-приложения. При проведении первого анализа производительности и масштабируемости было выявлено поведение, показанное на Рис. 4. Очевидно, наши данные оказались значительно выше кривой, полученной из теории массового обслуживания. Это был очевидный признак немасштабируемого поведения, нуждаю щегося в оптимизации. Однако для этого было необходимо сначала определить причину проблем с масштабируемостью.

Рис. 4 Поведение времени отклика в примере Java-приложения

Вообще, соревновательные условия могут возникать и в рамках одного приложения. В среде Java сборка мусора, являющаяся централизованным сер висом, – один из возможных источников проблем с масштабируемостью. Для выбора направления, в котором будут предприниматься шаги по оптимизации, важно определить источник проблем: следует ли искать конкретные конкурентные условия в конкретных приложениях? Или лучше сосредоточиться на эффективном использовании памяти?

Для выявления источника проблемы и нахождения подходящего решения в следующих разделах мы попробуем количественно охарактеризовать ожидаемое влияние процесса сборки мусора на среднее время отклика для заданных системных условий и приложений.

Сборка мусора в среде Java

Управление памятью путем сборки мусора – один из краеугольных камней Java-программирования и среды выполнения Java. На то есть веская причина, так как непоследовательное выделение и освобождение памяти – это больное место всех языков программирования, полагающихся на управление памятью посредством кода (т.е. эксплицитное выделение и освобождение памяти). JVM автоматически управляет созданными объектами; в частности, она обеспечивает корректное удаление объектов. За удаление объектов отвечает поток сборки мусора, для работы которого, разумеется, требуется определенное количество системных ресурсов. Для выполнения потока сборки мусора требуются не только процессорные ресурсы; алгоритмы сборки мусора также зависят от некоторой степени эксклюзивного доступа к динамической памяти JVM (подробнее об управлении памятью см. в выноске ниже). Во время эксклюзивного доступа все потоки приложения на той же JVM останавливаются – подобное поведение можно представить себе как “всемирную минуту тишины”.

На Рис. 5 проиллюстрирован процесс сборки мусора на JVM с двумя характерными параметрами. В верхней части рисунка показана зависимость выделенной динамической памяти от времени. В нижней части показано соответствующее количество активных потоков.

Рис. 5 Иллюстрация сборки мусора с точки зрения динамической памяти и числа активных потоков

Управление памятью в среде Java: динамическая память и сборка мусора В среде программирования и среде выполнения Java функции по выделению и освобождению памяти выполняются системой. В частности, не требуется какое-либо явное освобождение памяти в коде приложения. Новые объекты создаются в общей области памяти, называемой “динамической памятью”. После завершения работы с объектами они остаются в динамической памяти в виде “мусора”. Время от времени системное приложение – “сборщик мусора” – проверяет динамическую память, идентифицирует неиспользуемые объекты и удаляет их (как показано в верхней части Рис. 5). Для оптимизации процедуры сборки мусора были разработаны сложные алгоритмы*. * Для получения подробной информации о доступных алгоритмах см. http://java.sun.com/docs/hotspot/gc1.4.2/index.html или http://www.ibm.com/developerworks/java/jdk/linux/50/sdkandruntimeguide.lnx.en.html.

Рассмотрим происходящее в верхней части подробнее. Слева имеется некоторое количество выделенной динамической памяти и несколько активных пользователей, выполняющих Java-приложения. Потоки, связанные с этими приложениями, создают в процессе своей работы объекты в динамической памяти. Следовательно, объем использованной динамической памяти, обозначенный красной линией, увеличивается. Большинство из созданных объектов требуются лишь временно, однако остаются в виде “мусора” в динамической памяти, так как они не освобождаются приложением эксплицитно. Следовательно, доступный объем динамической памяти сокращается. По достижении определенного критического уровня (в зависимости от фактической стратегии сборки мусора конкретной JVM) инициируется сборка мусора. При сборке мусора такие объекты удаляются из динамической памяти, в результате чего память освобождается для дальнейшей работы. Этот процесс повторяется непрерывно в течение работы системы. При отсутствии утечек памяти (которые обычно образуются в Java при сохранении ссылок на неиспользуемые объекты) система находится в стабильном состоянии.

Теперь рассмотрим подробнее нижнюю часть рисунка, где показано количество активных потоков (на оси Y). Для простоты предположим, что сборка мусора выполняется с полным эксклюзивным доступом (единственного) потока – “сборщика мусора”. Это приводит к возникновению “минуты тишины”: во время сборки мусора активен только один поток. Потокам, которые были активны до наступления этого момента, и новым заявкам приходится ожидать своей очереди. Теперь рассмотрим последствия с точки зрения времени отклика приложений.

Влияние сборки мусора на время отклика приложений

Для начала расширим простой пример, приведенный на Рис. 1. На Рис. 6 в дополнение к временным шкалам пользовательской активности добавлена временная шкала сборки мусора.

Рис. 6 Иллюстрация увеличения времени отклика из-за сборки мусора

“Сборщик мусора” в этом примере активизируется один раз. На рисунке видны две ситуации, в которых время отклика приложения превышает непосредственное время обслуживания. Первый случай (помечен на Рис. 1 как “Увеличенное время обслуживания”) был рассмотрен ранее. Он проистекает из конкуренции между двумя заявками за один обслуживающий узел. Вторая ситуация (помеченная на Рис. 6 как “Увеличение времени отклика из-за сборки мусора”) вызвана работой сборщика мусора: ожидать приходится как ранее активным потокам, так и новым заявкам. С качественной точки зрения совершенно ясно, что это приводит к характерному увеличению времени отклика приложения. Выразим это увеличение количественно, обратившись к эффекту остановки на сборку мусора и скапливания заявок во время этой остановки.

Эффект остановки на сборку мусора

Начнем с эффекта, непосредственно видного на Рис. 6: сборка мусора приводит к приостановке процесса обработки заявок на некоторое время. При этом увеличивается время отклика для всех пользователей, заявки которых уже обрабатываются, равно как и для пользователей, сформировавших заявки в период сборки мусора. Эта задержка не влияет непосредственно только на тех пользователей, которые в течение всего периода сборки мусора “размышляют”. Если мы положим вероятность получения заявки от пользователя постоянной во времени, можно аналитически вычислить увеличение среднего времени отклика. Ниже будут последовательно рассмотрены некоторые из этих шагов, так как эта процедура дает весьма поучительные результаты, которые пригодятся нам позднее. (Однако следует учесть, что предположение о равно мерном распределении заявок не соответствует действительности, поскольку само распределение подвержено влиянию остановок из-за сборки мусора; этот дополнительный эффект будет более подробно рассмотрен в следующем разделе, где речь пойдет о скапливании заявок в период сборки мусора.)

Расчет включает в себя немного алгебры. Здесь важно понимать используемые обозначения, поэтому начнем с описания соответствующих им параметров:

• n – количество пользователей.
• r – чистое время обслуживания.
• d – время размышления пользователя.
• gc – продолжительность единичного акта сборки мусора.
• fgc – периодичность сборки мусора (число актов сборки мусора за единицу времени).

Предположим, что имеется n пользователей. С постоянной во времени вероятностью пользователи инициируют заявки с чистым временем обслуживания r, а затем ожидают в течение времени d (время размышления пользователя). Эта ситуация показана в левой части Рис. 7. Затем наступает “минута тишины”, инициируемая процессом сборки мусора. На рисунке представлен случай, в котором продолжительность сборки мусора gc меньше времени размышления пользователя d.

 

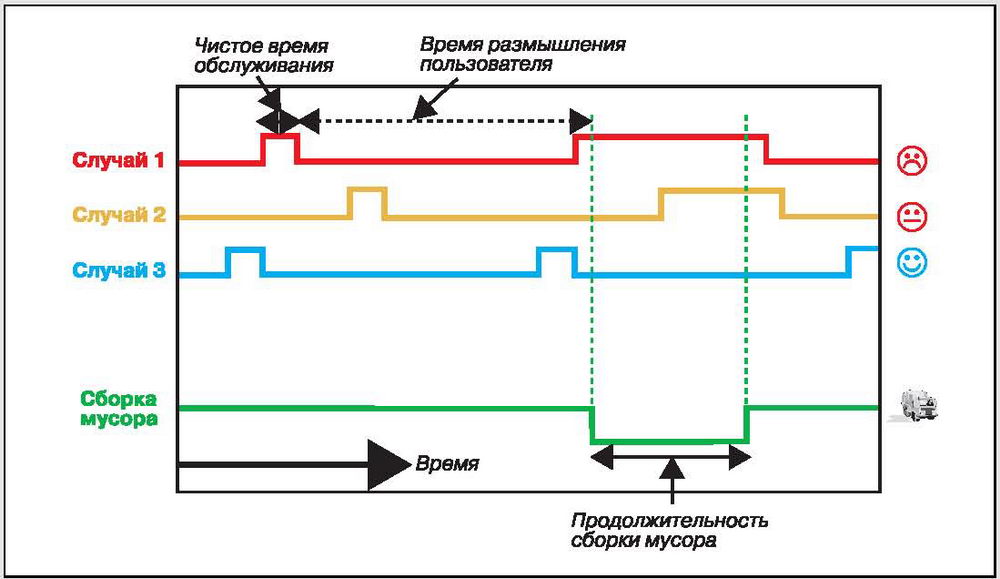
Рис. 7 Расчет эффекта остановки на сборку мусора: троякое воздействие на пользователей

С точки зрения пользователей имеет место один из трех вариантов:

1. Сборка мусора происходит во время обработки заявки на обслуживание (случай 1). Это приводит к увеличению общего времени обслуживания Dr₁, равному времени gc. Поскольку предполагается, что заявки пользователей равномерно распределены во времени, также можно определить количество пользователей, сталкивающихся с этой ситуацией, а именно n₁ = n * r / (d+r).
2. Сборка мусора происходит в течение времени размышления, однако заявка на обслуживание формируется во время сборки мусора (случай 2). Затрагивается n₂ = n * gc / (d + r) пользователей. Эти пользователи испытывают все возможные задержки от 0 до gc, со средним значением Dr₂ = gc / 2.
3. Сборка мусора происходит в течение времени размышления пользователя и заканчивается до окончания времени размышления (случай 3). Число таких удачливых пользователей равно n₃ = n * (d-gc) / (d + r).

Теперь обобщим полное увеличение времени отклика для каждого пользователя при однократной операции сборки мусора, как показано на Рис. 8.

Рис. 8 Уравнение расчета общего увеличения времени отклика для каждого пользователя в случае отдельной операции сборки мусора

Эквивалентный расчет можно выполнить для случая gc > d.

С периодичностью сборки мусора fgc мы получим среднее время отклика R_av = r + Dr, как показано на Рис. 9.

Рис. 9 Уравнения расчета среднего времени отклика для системы с периодичностью сборки мусора fgc

Этот результат описывает среднестатистическое увеличение времени отклика из-за остановок на сборку мусора. Рассмотрим подробнее выражение в скобках. “1” соответствует чистому времени обслуживания. Второй член fgc * gc – доля времени, затраченная на сборку мусора. Это можно назвать “наивной” оценкой эффекта: “если продолжительность сборки мусора составляет 2% от времени исполнения, время обработки увеличивается на 2%”. Конечно, это неверно из-за третьего члена. Для gc d это квадратичный член в gc. Очевидно, что как только продолжительность сборки мусора превысит чистое время обслуживания более чем вдвое, он будет превосходить первый член. Для gc d мы переходим к нижнему уравнению, являющемуся линейным продолжением увеличения времени отклика при большой продолжительности сборки мусора.

На Рис. 10 проиллюстрирован результат для одного примера. Он показывает зависимость относительного среднего времени отклика от длительности одной операции по сборке мусора. (Относительное время отклика – просто среднее время отклика R_av, разделенное на чистое время обслуживания r. Этот показатель позволяет получить более точное представление об изменении времени отклика в единицах чистого времени обслуживания, независимо от фактического абсолютного значения этого времени.) График показывает, что происходит, когда продолжительность каждого периода сборки мусора увеличивается, в то время как остальные параметры (время размышления пользователя d, чистое время обслуживания r и периодичность сборки мусора fgc) остаются неизменными. В этом примере время размышления пользователя установлено равным приблизительно 10 секундам. Поэтому сначала наблюдается квадратичная зависимость, описанная первым уравнением (gc d), вплоть до продолжительности сборки мусора, равной 10 секунд, и линейное продолжение для больших значений продолжительности. Видно, что среднее время отклика существенно зависит от продолжительности процесса сборки мусора.

Рис. 10 Эффект остановки: расчетное время отклика в зависимости от продолжительности отдельной операции сборки мусора

До сих пор мы не учитывали детали конкретных стратегий сборки мусора, предусмотренных в различных JVM. Подробное рассмотрение доступных алгоритмов также выходит за рамки настоящей статьи⁴. На основании Рис. 10 мы можем сделать ряд базовых выводов в этом отношении. В нескольких реализациях JVM доступны стратегии сборки мусора, приводящие к выполнению двух классов сборки мусора: “малому” и “полному” прогонам этого процесса. Как правило, малые прогоны сборки мусора значительно короче полных. Следовательно, в основном влияние с точки зрения увеличения времени отклика оказывается полными прогонами сборки мусора, а эффектом от малых прогонов можно пренебречь (возможны исключения, когда продолжительность малой сборки мусора сравнима с чистым временем обслуживания или превосходит его, а также, очевидно, когда полные прогоны сборки мусора отсутствуют вообще).

⁴ Для получения информации относительно доступных алгоритмов см. http://java.sun.com/docs/hotspot/gc1.4.2/index.html или http://www.ibm.com/developerworks/java/jdk/linux/50/sdkandrun-timeguide.lnx.en.html.

Теперь применим уравнение для расчета среднего времени отклика в приведенном выше примере Java приложения, которое сравнивалось с прогнозом теории массового обслуживания на Рис. 4. Результат показан на Рис. 11. Если подставить конкретные значения для приложения в первое уравнение на Рис. 9, получим ожидаемое увеличение вследствие остановок на сборку мусора, обозначенное приведенной кривой. Некоторое увеличение времени отклика, конечно, является прогнозируемым, однако порядок эффекта лишь в незначительной степени объясняет поведение приложения. Очевидно, отсутствует какая-то компонента. Один возможный, хотя и преждевременный, вывод заключается в том, что к увеличению времени отклика сверх спрогнозированной задержки приводит некоторая особенность, изначально присущая рассматриваемому приложению. Однако в следующем разделе будет продемонстрировано, что учтены еще далеко не все последствия сборки мусора.

Рис. 11 Ожидаемое увеличение времени отклика вследствие остановки на сборку мусора

Эффект накопления заявок при сборке мусора

До сих пор мы предполагали, что заявки на обслуживание распределены во времени равномерно. Сборка мусора нарушает это распределение. Посмотрим, что происходит в системе со стабильной нагрузкой при запуске процесса сборки мусора. Эта ситуация изображена на Рис. 12, где показана зависимость количества ожидающих заявок от времени. Начнем слева, с ситуации стабильной нагрузки: в системе обрабатывается определенное количество заявок. В устойчивом состоянии количество поступающих заявок совпадает с числом обработанных заявок. Таким образом, количество ожидающих заявок во времени остается постоянным. Когда объем занятой динамической памяти превышает некую отметку, инициируется сборка мусора, меняющая картину. Все новые заявки должны помещаться в очередь ожидания. Поскольку заявки не обслуживаются, количество ожидающих заявок устойчиво увеличивается вплоть до завершения сборки мусора. В результате очередь заявок растет. По завершении сборки мусора начинается разбор отложенных заявок. Со временем, по мере обработки заявок из очереди вновь активными обслуживающими узлами, система возвращается в стабильное состояние. (В ситуации случайного времени размышления это стабильное состояние напоминает начальную ситуацию. В случае фиксированного времени размышления результат иной: в системе наблюдаются колебания нагрузки, отмеченные на Рис. 12 вопросительными знаками.) Поэтому возникает следующий вопрос: как сборка мусора влияет на формирование очереди ожидания или накопление заявок, приводящие к увеличению времени отклика?

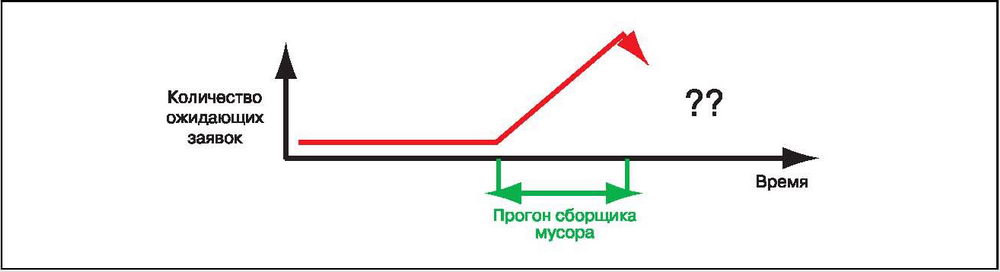
Рис. 12 Эффект накопления заявок при сборке мусора

С качественной точки зрения нетрудно понять, что влияние эффекта накопления заявок должно быть существенным. Предположим, что в начальной ситуации системная нагрузка имеет конкретное, разумное значение – например, 40%. Если компьютер четырехядерный, мы можем использовать увеличение времени отклика, ожидаемое для идеальной (M/M/4) системы массового обслуживания, обозначенное сплошной линией на Рис. 2. Исходя из этого, ожидается лишь небольшое увеличение времени отклика (несколько процентов) по сравнению с чистым временем обслуживания вследствие конкуренции за ограниченные ресурсы процессора. Теперь рассмотрим ситуацию, где сборка мусора закончена, а обслуживающие узлы снова активированы. Для каждого обслуживающего узла в любой момент будет готова заявка для обработки. Поэтому в течение некоторого времени будет наблюдаться очень высокая системная нагрузка, которая будет явно ближе к 100%, чем к 40%. На Рис. 2 мы видим, что это явление приводит нас в область, где ожидаемое увеличение времени отклика очень велико даже в идеальной системе. Проще говоря, сборка мусора временно переводит систему в состояние с очень высокой нагрузкой, что, очевидно, оказывает неблагоприятное влияние на среднее время отклика.

Наша задача состоит в количественном измерении влияния на время отклика эффекта накопления заявок. В отличие от эффекта остановки, выполнение простого аналитического расчета по этому показателю не представляется возможным. Вместо этого мы должны обратиться к полному моделированию системы, которое дает необходимые ответы для конкретных условий приложений, стратегии сборки мусора и системной среды. Сюда входит эффект накопления заявок, а также эффект остановки и общее увеличение времени отклика из-за конкуренции за процессорные ресурсы, рассмотренное ранее в контексте теории массового обслуживания.

Для получения количественного описания организуем моделирование по методу Монте-Карло. Во времени отслеживается работа n пользователей. Они формируют заявки на обслуживание, которые обрабатываются за чистое время обслуживания r обслуживающими узлами, количество которых равно m. Между заявками каждый пользователь неактивен в течение некоторого среднего времени размышления d. Сборка мусора вводится как периодические паузы в работе обслуживающих узлов, где прогнозируются две категории сборки мусора с различной продолжительностью gm и gc (малые и полные прогоны сборки мусора). Состояние этой системы отслеживается в течение многих циклов сборки мусора; активность формирования заявок по каждому пользователю фиксируется с достаточным временным разрешением (в частности, активные заявки остаются активными в течение остановок на сборку мусора). Увеличение времени обслуживания из-за сборки мусора рассчитывается исходя из зависимости общего времени пребывания заявок в активном состоянии от общего числа заявок.

На Рис. 13 проиллюстрировано моделирование простого примера. Показана нагрузочная ситуация во времени для 20 пользователей, работающих на четырехпроцессорном компьютере. Количество ожидающих заявок обозначено сплошной линией. Короткие линии изображают активные заявки каждого из 20 пользователей (каждая группа горизонтальных линий соответствует одному пользователю), разделенные (фиксированным) временем размышления. Слева мы начинаем со стабильной ситуации с двумя одновременными заявками (отметим, что ради ясности картины начальное распределение не было рандомизировано; вместо этого предполагается, заявки формируются пользователями последовательно). Через некоторое время инициируется процесс сборки мусора, обозначенный зеленым прямоугольником. В ходе сборки мусора количество ожидающих заявок увеличивается. Затем обработка заявок начинается снова, однако к этому моменту практически все пользователи уже оказываются в очереди ожидания. В результате возникает эффект синхронности, при котором обслуживание почти всех пользователей будет начато в одно и то же время. Система обрабатывает всю совокупность заявок в условиях максимальной нагрузки. Из-за синхронности система может достигнуть состояния, когда в очереди ожидания заявок нет, а следующая заявка поступает только через некоторое время. Следовательно, за фазой максимальной нагрузки следует период с нулевой нагрузкой. Разумеется, одним из последствий синхронности является совпадение момента окончания времени размышления в коротком промежутке для всех пользователей. После этого наблюдается переход от нулевой нагрузки к высокой нагрузке. В данной модели используется фиксированное время размышления пользователя; следовательно, колебания нагрузки повторяются снова и снова. Отметим, что если время размышления пользователя выбирается случайным образом, система способна вернуться к стабильному состоянию, показанному слева, после нескольких погашенных колебаний.

Рис. 13 Моделирование по методу Монте!Карло для простого примера нагрузочной ситуации

Исходя из результатов моделирования, мы теперь можем вычислить среднестатистическое увеличение времени отклика для данной системной нагрузки. Естественно, моделирование необходимо проводить для условий, определяемых конкретным приложением, стратегией сборки мусора и системной средой. На Рис. 14 показан результат моделирования относи тельного времени отклика в зависимости от нагрузки для вышеописанного примера Java-приложения. Видно, что данные измерений полностью соответствуют модели. Можно сделать вывод, что увеличение времени отклика, наблюдаемое в этом случае, в самом деле вызвано сборкой мусора. С этим результатом у нас теперь достаточно данных, чтобы предпринять следующие шаги по оптимизации приложения и системы. Мы знаем, что деградация производительности системы обусловлена факто рами, связанными с использованием памяти и/или управлением памятью. В одном из следующих разделов мы приведем ряд рекомендаций по устранению таких проблем.

Рис. 14 Результаты моделирования относительного времени отклика по сравнению с данными и теоретическим прогнозом

Перед этим, однако, стоит обратиться к практической проблеме. Несомненно, нам пригодились бы результаты полного моделирования работы приложения в каждой конкретной ситуации. Однако весьма неудобно выполнять моделирование всякий раз, когда требуется выяснить, вызвано ли наблюдаемое увеличение времени отклика для произвольного приложения сборкой мусора. Лучше иметь простую формулу, которую можно было бы, например, применить в электронной таблице. Более того, было бы правильно получить более конкретное и в то же время простое (по сравнению с полным моделированием) представление о механизме, приводящем к увеличению времени отклика.

Этим требованиям удовлетворяет эффективная модель сборки мусора, которой посвящен следующий раздел.

Эффективная модель сборки мусора

Моделирование по методу Монте-Карло описывает как время остановки на сборку мусора, так и накопление заявок. Его недостатком, однако, является потребность в создании полной модели для каждого нового набора параметров, в то время как аналитическая формула времени остановки дает прямой ответ для всех случаев. Было бы удобно иметь аналогичную формулу, включающую в себя основные результаты полного моделирования, в частности, эффект накопления заявок. Модель, описанная ниже, дает неплохое приближение к полному моделированию. Основная идея проиллюстрирована на Рис. 15.

Рис. 15 Эффективное время полной сборки мусора

Уравнения времени остановки были получены исходя из действительной (полной) продолжительности сборки мусора. Теперь добавим эффект накопления заявок путем увеличения эффективного времени сборки мусора. В остальном сохраняется аналитический расчет изменения времени отклика, описанный для чистого эффекта остановки. Вместо реального полного времени сборки мусора, в котором учитывается только время остановки на сборку мусора, будем использовать эффективное полное время сборки мусора, учитывающее эффект накопления заявок. Это эффективное полное время сборки мусора – сумма реального времени сборки мусора и времени, требуемого на обслуживание очереди, сформировавшейся в течение времени реальной сборки мусора. Используется уравнение, показанное на Рис. 16, где n – число пользователей в системе, а CPUs – число обслуживающих узлов.

Рис. 16 Уравнение расчета эффективного времени полной сборки мусора

Затем путем введения эффективного полного времени сборки мусора в формулу, полученную для времени остановки на сборку мусора рассчитывается среднестатистическое время отклика R_av. В результате мы получаем систему уравнений, показанную на Рис. 17.

Рис. 17 Уравнения для расчета эффективной продолжительности сборки мусора и результирующего среднего времени отклика

На Рис. 18 показано дополнительное влияние эффекта скапливания заявок при введении эффективной продолжительности сборки мусора. Так, маленькие стрелки обозначают чистую и эффективную продолжительность сборки мусора. Изменение времени gc и результирующее изменение относительного времени отклика обозначены большими стрелками. Используется тот же пример, что и на Рис. 10, иллюстрирующий уравнения чистого времени остановки. Из этого мы получаем чистую (реальную) продолжительность сборки мусора, отмеченную на горизонтальной оси. По взаимозависимости относительного времени отклика и продолжительности сборки мусора она соответствует некоторому относительному увеличению времени отклика. На Рис. 11 было показано, что это увеличение не объясняет наблюдаемое поведение приложения. Теперь мы включаем в эффективное время сборки мусора время, необходимое для обработки очереди заявок, возникшей в результате сборки мусора. При этом время отклика существенно увеличивается, и получается результат, достаточно близкий к результату полного моделирования.

Рис. 18 Влияние эффективного времени сборки мусора на время отклика

Этот набор уравнений позволяет быстро получить оценку предполагаемого влияния сборки мусора на время ожидания пользователей. Необходимо подчеркнуть, что эта аппроксимация пригодна для средних системных нагрузок около 50-60%. Однако она должна быть достаточной для оценки того, может ли наблюдаемое увеличение времени отклика объясняться влиянием сборки мусора. Этот прогноз можно использовать как эмпирическое правило для оценки эффекта сборки мусора.

Мы достигли цели, указанной во введении: получен инструмент, позволяющий определить, вызвано ли ухудшение времени отклика пользователей методами использования памяти, либо проблема вызвана другими причинами, связанными с конкретным приложением. В следующем разделе приведен ряд общих рекомендаций по мерам на случай, если основным источником проблем является сборка мусора.

Рекомендации

Используя полученное выше эмпирическое правило, предположим, что в качестве первоисточника проблем со временем отклика приложения были названы факторы, связанные с использованием памяти. Что делать в этом случае? Какие меры предпринять? Ниже приводится ряд общих рекомендаций – сначала с точки зрения Java-разработки, затем с точки зрения системного администрирования (т.е. настройки JVM).

Java-разработка

Если сборка мусора приводит к снижению производительности, задачу Java-разработки можно сформулировать в двух словах: экономия памяти.

Следует создавать только действительно необходимые объекты, поскольку на сборку каждого неиспользованного объекта время тратится впустую. Если последовательно выполняются идентичные операции, для которых требуются объекты одного типа, рассмотрите возможность повторного использования объектов вместо их создания и отбрасывания. Размер объектов следует свести к минимуму. Для этого на фазе разработки могут потребоваться дополнительные меры по определению объема памяти, действительно необходимого во время выполнения, однако эти усилия будут щедро вознаграждены тем, что исчезнет необходимость в постоянном контроле неиспользованной памяти.

Особо тщательного подхода требует разработка кэша. В отличие от других сред программирования, при сборке мусора ресурсы процессора и памяти оказываются связанными. В Java эти ресурсы не являются независимыми. Экономия времени в результате кэширования должна перевешивать накладные расходы на сборку мусора.

Наконец, немаловажно избегать утечек памяти. Утечки памяти в Java обычно возникают в форме неиспользованных, но не освобожденных ссылок. Отсюда напрямую следует многократная бесполезная обработка и, возможно, даже копирование таких объектов сборщиком мусора. В конечном счете, типичным следствием утечки памяти является истощение ресурсов памяти, за которым следует регулярная, но безуспешная полная сборка мусора и окончательное исчерпание памяти JVM. Этого, конечно, следует избегать. Устранение утечек памяти, следовательно, имеет наивысший приоритет, когда память является лимитирующим ресурсом.

Настройка JVM

Задача администратора JVM состоит в минимизации двух количественных характеристик: частоты (полной) сборки мусора и, что еще важнее, продолжительности этой операции. Эти величины можно контролировать путем выбора правильной стратегии сборки мусора и конфигурирования размера динамической памяти.

Как уже было сказано в описании уравнений времени остановки, продолжительность сборки мусора оказывает существенное влияние на время отклика. В частности, следует помнить, что в стратегиях, в которых применяются малые и полные прогоны сборки мусора, влиянием малых прогонов на время отклика обычно можно пренебречь (в отличие от полных прогонов). Эти стратегии сборки мусора доступны для разнообразных JVM, например, JVM Sun. Стоит задуматься об использовании стратегий “параллельной” или “одновременной” сборки мусора. Перенос части работы из длительной процедуры полной сборки мусора в малые прогоны, по крайней мере, сокращает эффективную (с точки зрения времени отклика) продолжительность сборки мусора и также должен сократить периодичность этого процесса. Еще лучше, если часть или все функции, выполняемые при малой сборке мусора, будут осуществляться с минимальным эксклюзивным доступом к динамической памяти (или, в идеальном случае, полным отсутствием такого доступа). Для получения подробной информации о стратегиях сборки мусора для конкретных JVM см. документацию от поставщиков JVM⁵. Разумеется, не стоит рисковать стабильным функционированием рабочей системы, экспериментируя с непроверенными настройками или стратегиями сборки мусора. (Рекомендации для SAP-систем с различными комбинациями платформ/JVM приведены в SAP-нотах 634689 и 723909.)

⁵См. http://java.sun.com/docs/hotspot/gc1.4.2/index.html или http://www.ibm.com/developerworks/java/jdk/linux/50/sdkandrun timeguide.lnx.en.html.

Параметром, напрямую влияющим на общую продолжительность сборки мусора, является заданный размер динамической памяти. В наше время 64 разрядных компьютеров не существует реальных пределов задаваемого объема динамической памяти (разумеется, она должна вмещаться в доступную физическую память). Большая динамическая память может казаться привлекательной, однако это решение пригодно только в том случае, если размер динамической памяти настолько велик, что полный прогон сборки мусора никогда не потребуется. Пока это не так, преимущество минимизации частоты сборки мусора более чем перевешивается увеличением ее продолжительности. Это непосредственно следует из уравнений времени остановки, где периодичность сборки мусора является линейной, а зависимость от продолжительности сборки мусора – квадратичной. Следовательно, лучше создать несколько серверных узлов, чем один, но с огромной динамической памятью. Оптимальный размер динамической памяти, конечно, зависит от конкретного приложения. Опять же, обратитесь к информации, приведенной в SAP нотах 634689 и 723909, содержащих рекомендации по конфигурированию для различных комбинаций плат форм и JVM.

Заключение

После прочтения статьи у читателя должно сформироваться четкое представление о воздействии процесса сборки мусора в среде Java на время отклика пользователя, о механизмах и последствиях этого процесса, а также о возможностях по оптимизации среды.

Начальной точкой послужил анализ ожидаемого поведения времени отклика пользователей в идеальной теоретической системе под увеличиваемой системной нагрузкой. Этот прогноз служит эталонным тестом для определения того, ведет ли себя система под нагрузкой как идеальная масштабируемая система, или в ней имеется проблема со временем отклика.

Затем был рассмотрен принцип действия сборки мусора и механизмы, влияющие на заявки пользователей. После этого пояснялось влияние времени остановки на сборку мусора, которое является прямым последствием эксклюзивного доступа процесса сборки мусора к динамической памяти. Было показано, что влияние сборки мусора не ограничивается эффектом паузы: заполнение очереди заявок во время сборки мусора приводит к возникновению периода высокой загрузки, существенно отражающегося на времени отклика пользователей в интервале обработки заявок из этих очередей после завершения сборки мусора.

В дополнение к качественному описанию этих двух эффектов, были представлены и их количественные следствия, полученные аналитическим расчетом и системным моделированием соответственно. Модель эффективной сборки мусора, построенная на основе этих данных, представляет собой удобный инструмент для принятия непростого решения о том, вызвана ли проблема со временем доступа использованием памяти, или же она связана с другими присущими приложению соревновательными условиями? Теперь для системы (вплоть до умеренной системной нагрузки) можно получить конкретную оценку ожидаемого изменения времени отклика из-за сборки мусора.

Если сборка мусора оказывается ведущим фактором увеличения времени отклика, последствия для Java-разработки и управления JVM очевидны: следует экономить память и минимизировать продолжительность полной процедуры сборки мусора. Мы надеемся, что общие рекомендации, приведенные в последнем разделе, окажутся полезными на пути к системе, в которой приложения работают с оптимальной производительностью.